ADS

AVL Tree¶

AVL的insert¶

递归插入构建AVL Tree：当左子树和右子树都已经在插入后确定为平衡树，则转换为下图问题：
（先将原问题转换为子问题，再解决子问题 / 先解决子问题，再解决原问题）

在实际模拟中，先按二叉树插入，随后从沿着插入路径从下到上地检查路径上每个节点的balance factor，哪个节点出现问题，就从此节点开始看是RR情况还是RL情况

RR、LL、RL、LR均指的是不平衡发生的插入结构。其中RR需左旋处理，LL需右旋处理，RL、LR可自下而上地分别调用成RR、LL的处理方式

复杂度分析：考虑单次（某次）操作所需的最坏时间复杂度：n个元素所能得到的最高AVL树的高度是多少<==>已知高度求最少需要的元素个数

AVL的delete¶

与插入类似，进行递归地删除。当遇到要删除的目标节点时，递归调用删除左子树上key等于最大值的节点，并替换，最后检查平衡性

T->Left=Delete(T->Left,leftMax);
/*after deletion the tree structure is changed*/

Delete a node v from an AvL treeT1, we can obtain another AvLtree T2. Then insert v into T2,we can obtain another AvLtreeT3. Which one of the folowing statements is(are) true?
1、If v is a leaf node in T1, then T1 and T3 might be different.
2、If v is not a leaf node in T1, then T1 and T3 must be different.
3、If v is not a leaf node in T1, then T1 and T3 must be the same.

Splay Tree¶

查找操作¶

单次查询的时间复杂度仍可能为O(N)

在找到目标结点后，通过以下操作进行旋转，直到目标节点成为根节点为止：
（每次考虑查找结点与其父亲、祖父的位置关系）

zig zag：一次LR或一次RL操作
zig zig：连续两次LL或连续两次RR操作（先转P再转X）

插入操作¶

先按照二叉搜索树的插入方式插入，随后按照splay树的查找方式将新插入的节点旋转成根节点。

删除操作¶

Amortized Analysis¶

For splay tree:

分析方法¶

当满足在系列操作最开始的时候Potential Function的值最小就是合理的

一旦势能函数的合理性得到保证，那么重点就在于每一项的构造上，使得其加和易于计算（能排除特殊情况的突变干扰）

事实上，虽然始末状态的势能差值必为非负数，但某一步操作导致的势能差值可能为负数

注意，在zig-zag和zig-zig操作中不应该有常数项，因为不知道zig-zag和zig-zig具体分别会进行多少次

典型数据结构的复杂度¶

Heap:

	INSERT	DELETE
worst	O(logN)	O(logN)
amortized	O(logN)	O(1)

Red-Black Tree¶

第五条更加精准的定义是：Every path from a node to a NULL pointer must comtain the same number of black nodes（这避免了普通二叉树退化成链表的情况)

插入操作（可用循环解决）¶

判断插入的红结点的叔叔的颜色与朝向

将每个插入的新节点记为红色，先用普通BST的插入方式插到最底部，显然，当其父节点为黑色时插入完成。

需要考虑的仅有两大类情况：插入节点的叔叔是红色还是黑色。（以上带子树的树列举的是case1在迭代过程中可能出现的一般情况）

case 1：转换成祖父节点（及其子树视为整体）为新的红色节点插入，不断向上迭代直到不会与“红节点的子节点必为黑”冲突（父节点为黑或成为根节点染黑）。这是唯一需要迭代的case。

case2.1：2.1、2.2的区别在于子节点和叔父节点的朝向是否相同，若相同则旋转至不同（case2.1->case2.2）再处理。

case2.2：两次操作：转一次、换染一次。转完之后会发现右子树的bh大于左子树，则通过父亲和儿子的颜色交换即可解决所有问题。

删除操作¶

删除一个节点时rotation的次数为O(1)

本质上是删除叶节点，因为Replace操作实际上是键值的替换，被删除节点的颜色是不变的，最终要丢掉的还是叶节点。

当叶节点是红色时，直接丢掉

2.当叶节点是黑色时，总体而言有两大类情况：被删节点的兄弟是红色还是黑色

兄弟是红色（转）
兄弟是黑色
- 兄弟的双儿子是黑色（将缺少的黑色向上转移）
- 兄弟的远端儿子是黑色，近端儿子是红色（转）
- 兄弟的远端儿子是红色（转）

case1：x的兄弟是红色¶

换色是为了防止10是红色的这种情况，换色是必须的

case2.1：x的兄弟及兄弟的两个儿子均为黑色且x的父亲为红色¶

case2.2：x的兄弟及兄弟的两个儿子均为黑色且x的父亲为黑色¶

这里的染色操作使整个右子树的高度减少了1，那么相当于要进行删除节点（前）的补黑操作。

case3：x的兄弟是黑色，x兄弟的远端儿子是黑色，近端儿子是红色¶

case4：x的兄弟是黑色，x兄弟的远端儿子是红色，近端随意¶

若此例子中的7是黑的，则可以看出转完后改色的重要性了

B+ Tree¶

基本定义¶

需要注意的是非叶节点（nonleaf node）的键值是其整个中/右子树上的最小值（需要在叶节点中找出）

无论degree是多少，查找的时间复杂度都是O(logN)

插入操作¶

这里的split是指将一个满的（父）节点分成两个节点，并更新节点的儿子与键值

Leftist Heaps¶

why：两个堆的元素个数总数为N时，对两个普通堆进行合并，相当于调整一个初始杂乱的数组，需要O(N)的复杂度

Npl最终数出的是步数（从父节点到子节点记为一步）

当某个节点的左儿子为NULL时，检查左偏树时要考虑NULL的Npl

合并操作-recursive¶

概括而言对于极小堆就是：选择两个堆中的根值较小者，将其右儿子和另一个堆合并得到的新的根作为右儿子

这样保证了每次合并时新的作为根的堆的左子树不变

if(H1->Element<H2->Element){
    H1->Right=Merge(H1->Right,H2);
    update children;
    update Npl;
    return H1;
}else{
    H2->Right=Merge(H2->Right,H2);
    update children;
    update Npl;
    return H2;
}

合并操作-iterative¶

随后还有从下到上的交换左右儿子操作

Step 1: Sort the right paths without changing their left children

Step 2: Swap children if necessary(bottom->top，不用考虑根节点的左子树)

注意这里的“sort”是指最右路径的节点从上到下是依次递增的，每层循环决定最右路径上的一个节点及其左儿子。

最终右路径上的节点就是两个堆分别的右路径上的节点，所以可以用双指针来比较。

DeleteMin操作¶

删除根节点，得到两个堆，再将两个堆合并

典型结论¶

按顺序将含有键值1,2,···,$2^k-1$的结点从小到大依次插入左式堆，那么结果将形成一棵完全平衡的二叉树。
按顺序将含有键值1,2,···,$2^k-1$的结点从小到大依次插入斜堆，那么结果将形成一棵完全平衡的二叉树。

Skew Heap¶

与左倾堆对比就是每次操作的复杂度可能提升，但amortized bound不变，且不需要判断是否要交换儿子、不需要存每个节点的Npl

每次操作复杂度不能确定原因是与Leftist Heaps不同，右路径总长度不超过logN

合并操作¶

只有右路径上的最大节点不需要交换儿子（作为递归的出口）

“右路径上的最大节点” 就是两棵树的右路径最底部节点中的较大者

循环的插入方式，每层循环：

比较原右路径对应深度的节点
交换将要作为“根节点”的节点的左右子树，且想象换之前父节点（新“根”）是有左子树的（因为换之前整个左子树是确定要变为右子树的，新的左子树不确定）
将新“根”插到左路径上（因为父节点比完后子树必交换，且左子树被整体保留地换到右边）

每个作比较的节点都是最初始两棵树的右路径上的节点，这些节点最后都会成为左路径上的节点。

摊还分析¶

两个引理：¶

Binomial Queue¶

基本定义¶

binominal queue（二项堆）：

binominal tree：

$B_{k}$的高度和儿子数均为k

二项堆是一个数据类型为节点指针的数组。数组中的每个元素是指向每个二项树的根节点的指针

二项堆可以唯一地被一组二项树表示，因为二项树的节点个数为2的次方数，而每一个数可以被唯一地表示为二进制数

数据结构¶

对于每棵二项树，其表示方法为LefttChildNextSibling，且根的每个子树应该是从左到右从大到小排列的：因为每次combine都会将与整棵树大小相同的树作为儿子，又考虑到是左儿右兄表示法，则从大到小排可避免遍历整个第二层

二项树操作-CombineTrees¶

二项堆操作-FindMin¶

优化时间

二项堆操作-Merge¶

首先要保证二项堆的每棵树已经排好序，这样便于合并两个数组时进行对齐

合并相当于两个二进制数的加法（得到一个新的唯一的二进制数）
这涉及到进位问题：当同时得到三棵相同高度的树时，可人为选择合并哪两颗作为进位，保留哪一棵

合并两个相同长度的二项堆需要的最坏时间是O(logN)：每棵树的合并时间为O(1)，最坏情况下每个二项堆有O(logN)棵二项树（这里的N是每个二项堆的节点总数）

需要注意的是这里循环终止的条件是根据合并后总的节点数H1->CurrentSize来判断的:
因为我们知道最后得到是queue的长度不会超过log(H1->CurrentSize)

二项堆操作-DeleteMin¶

这里图中的画法反了，每棵树应该是从左到右从大到小的顺序排列

其中 Remove $B_k$ 操作只需要将原二项堆相应位置的指针置为NULL即可，即删除最小值的时候会移除整棵对应的树

创建二项堆的复杂度分析¶

Aggregate Analysis：考虑每个需要进位的情况：1，11，111，1111，···，其分别周期性出现

Amortized Analysis：

这里的c unit时间是设置指针指向根节点(step=1)+合并的二项树次数(link=c-1)

Backtracking¶

Basic Idea¶

backtracking的本质是使用深度优先算法遍历所有可能的解的情况（这些情况通常为分支结构，可以用树来表示）

遍历每种子情况时是不用把每种约束情况都作为条件的的，而是通过特定的某种约束条件将所有可能取到的解遍历一遍，再考虑遍历过程中的剪枝或最后进行一次性的验证

八皇后问题¶

考虑4*4棋盘上的四皇后问题：

利用回溯找出所有满足八皇后条件的解：

void EightQueen( int row ) //initially row=0
{
    int col;
    if( row>7 ){
        Print();  
        count++;
        return ;    
    }

    for( col=0; col < 8; col++ )
    {
        if( notDanger( row, col )){ 
            chess[row][col]=1;

            EightQueen(row+1);          

            chess[row][col]=0; //已经考虑完一种完整的子情况，清零
        }
    }
}

传统的递归思路是无法打印出所有符合条件的解的

回溯思想的本质是：遍历筛查 + 一条路搜到底
即想走遍game tree的所有到达叶节点的搜索路线（将所有可能的情况考察一遍），但在搜索的过程中会进行剪枝判断，提前排除某些情况。

如何将每种可能解的遍历类比树的深度遍历？
深度优先搜索的递归思想：对起始情况的每种子情况分别进行深度优先遍历
重点即为判断起始情况有哪些子情况；子情况和原情况的区分（参数）的差别在哪里

加油站问题¶

X：存放从左到右每个点的位置坐标的数组，下标表示每个点的编号
D：存放所有两点之间距离的集合
left/right：X的下标，记录最新已知的两个点的编号

狼人与谎言问题¶

给定一组人，已知撒谎者和狼人的个数，每个人分别说某人是狼人或人类，求出按从大到小顺序排出的狼人序号。

遍历可能情况的方式：考虑每组狼人解中序号最大是多少

bool track(int i,int N,int M,int L)
{
    if(wolves.size()==M){
        return check(N,M,L);
    }

    for(int k=i ; k>M-wolves.size() ; k--) 
    {
        wolves.push_back(k);

        if(track(k-1, N, M, L)==true){
            return true;
        }else{
            wolves.pop_back();
        }   
    }
    return false;
}

这里并不是依次判断每个人是否是狼人来遍历一个二叉树，而是为了得到最大序号的一组解，考虑每个可能解（解森林中的每棵树）中狼人最大的序号是多少。

可以通过在每次调用dfs时传值来省去pop的操作

αβ/Minimax¶

α pruning¶

β pruning¶

复杂度优化¶

Divide and Conquer¶

基本思路¶

Master Method¶

another form：

Dynamic Programming¶

时间复杂度¶

状态转移开销*所有需要计算的状态数

Product of N Matrices¶

$m*n$的矩阵和$n*p$的矩阵相乘需要进行的操作数为$m*n*p$

$M_{ij}$表示的是计算过程中可能涉及到的子问题（从第i个矩阵乘到第j个矩阵）

考虑乘积的最后一步，可将其分解为两个子问题

Optimal Binary Search Tree¶

问题：给定一组words和其出现频率，求解（树结构下）最优平均搜索次数

本质上还是最优子结构问题：
递归的前提是子问题的结构中的i与j是任取的，且这些子问题都是尚待解决的（原问题），此时的“原问题”不再是找出完整的一组words的最优平均搜索次数

首先枚举地选择根节点，再分别计算出此情况下的最优平均搜索次数，再从中选取最小值。

对与形如$c_{ij}=min\{c_{i,l-1},c_{l+1,j}\}$这类的问题，可以直接使用如下循环来解决：

for(k=0;k<=n-1;k++) //从最小间隔开始算cij
    for(i=1;i<=n-k;i++)
        j=i+k;
        for(l=i;l<=j;l++) //比较得到min
            updateMin()

活动安排问题¶

这里的$a_i$是按照活动的结束时间从早到晚排序的

思路是考虑两种情况：要么安排最后一个活动，要么不安排

背包问题¶

无重复背包：给定一组物品，每个物品有相应的质量$w_k$与价值$v_k$。要求在给定背包容量的条件下求出背包中物品最大的总价值。

考虑是否将最后一个物品放入背包，则子问题：求解给定物品为原物品中的第1个到第k个，且背包容量为w时的最大价值$C[k,w]$

无后效性¶

给定下标从 0 开始的二维整数数组 questions ，其中 questions[i] = [pointsi, brainpoweri] 。

这个数组表示一场考试里的一系列题目，你需要按顺序（也就是从问题 0 开始依次解决），针对每个问题选择解决或者跳过操作。解决问题 i 将让你获得 pointsi 的分数，但是你将无法解决接下来的 brainpoweri 个问题（即只能跳过接下来的 brainpoweri 个问题）。如果你跳过问题 i ，你可以对下一个问题决定使用哪种操作。返回这场考试里你能获得的最高分数。

考虑从第i题开始到最后一题中能获得的最高分为 dp[i]，可二分为做第i题和不做第i题两类：
$$
dp[i] = max(dp[i+1],\space questions[i][0] + dp[next_available])
$$

状态机¶

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成两笔交易。

每次迭代为第i天的状态向第i+1天转换，以下变量记录每天各种状态下的最大收益

buy_1：完成一次买入
sell_1：完成一次完整交易
buy_2：完成第二次买入
sell_2：完成第二次完整交易

\[ sell_1 = max(sell_1,\space buy_1 + prices[i]) \]

\[ buy_1 = max(buy_1,\space -prices[i]) \]

\[ sell_2 = max(sell_2,\space buy_2 + prices[i]) \]

\[ buy_2 = max(buy_2,\space sell_1 - prices[i]) \]

注意，在考虑初始状态，即第0天的各个值时，可以把不可能出现的状态（buy_2，sell_1，sell_2）设为负无穷，因为只需要考虑在这些状态第一次合法出现时的赋值是否正确。

All-Pairs Shortest Path¶

跳板的个数依次增加，不断更新最优解

Greedy¶

基本定义¶

活动安排问题¶

这里的$a_i$是按照活动的结束时间从早到晚排序的

（也可以collecting the activity that starts the latest）

霍夫曼编码¶

霍夫曼树需要保证不存在一个编码是另一种编码的前缀

霍夫曼码长最多可以达到n-1位

All nodes either are leaves or have two children(full).

现给定一串字符及每个字符出现的频率，要求构造一棵trie树：

首先找到出现频率最小的两个字符作为最深的叶子，随后将这两个字符的频率之和作为新的节点及其频率
现在总的节点数量减一了，继续重复上述过程

这里复杂度的计算需要注意到堆的插入/删除都是O(logN)的复杂度

贪心证明¶

证明选出来的第一个元素是被最优解包含的
最优子结构证明：原问题的最优解必会导致子问题的最优解

注：在霍夫曼树问题中子问题指的即是合并两个节点后得到的n-1个节点中建立cost最小的树

NP-Completeness¶

一些典型问题¶

欧拉回路：必须经过图中每一条边恰好一次。（可以通过判断每个顶点的出度和入度是否相等来判断）

哈密顿环：必须经过图中每一个顶点恰好一次且最后返回起点，即路径长度等于顶点数。（没有简单的判定条件）

Halting Problem（非NPC）¶

图灵机¶

非确定性图灵机在每一步中面对很多种待选项时可以保证直接地（O(1)）选出通向结果的正确的一步。（直接决定树中每一层的选法）

NP问题¶

P；确定性图灵机可以在多项式时间内解决的问题
NP：非确定性图灵机可以在多项式时间内解决的问题，且确定性图灵机可以在多项式时间内验证

NP问题的一个例子：Hamilton Cycle

decidable problem：判定性问题，解空间为{0，1}，只需要得出对或者不对的结论

NP-Complete¶

NPC问题举例¶

旅行商问题/哈密顿回路问题¶

complete graph：图中的每一对顶点之间都有一条边相连

问题A可以归约（reduction）到问题B表示问题A比问题B简单

先证明TSP是NP问题，再证明HCP可以归约到TSP即可

要证明可规约，需要让HCP问题的一个实例转化成TSP的一个实例：

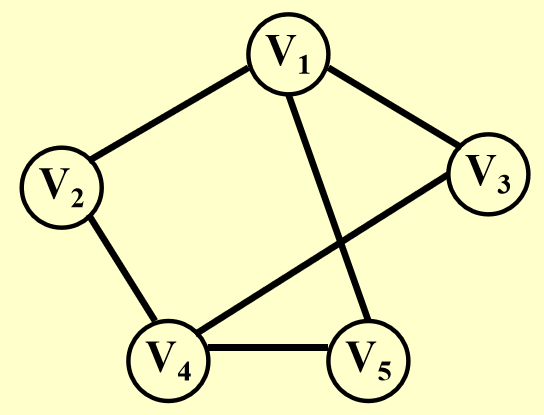
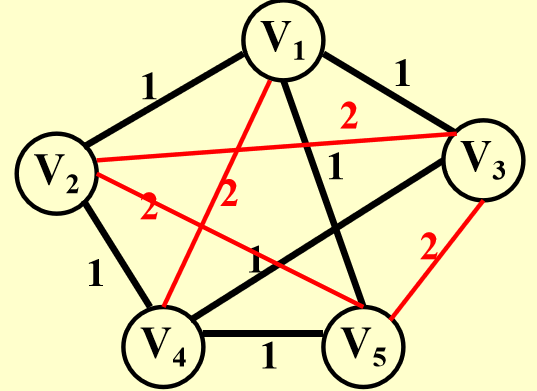
3-SAT问题（NPC）¶

satisfiebility：对于一个布尔代数式，存在一种变量的赋值方式使结果为真

3-SAT问题：每个子句（clause）都由三个变量组成（不同子句变量可能不同），且子句内部使用“或”连接。子句构成合取范式（conjunctive normal form）。

Clinque Problem and Vertex Cover Problem¶

注意这里没有说求最值，而只是给定了一个K作为边界

vertex cover：每条边至少有一个顶点在选出的点集中（应用十分广泛：在一个给定的关系网络中选出最少的信息传递者）

这里引入“补图”的概念，即原图的顶点不变，边取完全图下的补集

Language and Algorithm¶

如果算法A能够接受语言L中的每一个二进制字符串，并且能够拒绝不在L中的每一个二进制字符串，那么我们就说语言L是由算法A决定的。换句话说，算法A可以准确地识别哪些字符串属于L，哪些不属于L。

注意accept比decide要弱

L：问题的实例（例如哈密顿回路中设定的具体的某个图）

certificate：在实例下问题的一个具体发的解

co-NP问题¶

形式化举例¶

原问题：给定一个图 $ G $，是否存在一个哈密顿回路？
- 这个问题的语言 $ L $ 是所有包含哈密顿回路的图的集合。
补问题：给定一个图 $ G $，是否不存在哈密顿回路？
- 这个问题的语言 $ \overline{L} $ 是所有不包含哈密顿回路的图的集合。
原问题：给定一个整数 $ n $，是否是素数？
- 这个问题的语言 $ L $ 是所有素数的集合。
补问题：给定一个整数 $ n $，是否不是素数（即合数）？
- 这个问题的语言 $ \overline{L} $ 是所有非素数（包括合数和 1）的集合。

NP 和 co-NP¶

NP 类问题：这些问题是这样的问题，对于任何回答“是”的实例，存在一个多项式长度的证书使得可以在多项式时间内验证其正确性。
co-NP 类问题：这些问题的补问题在 NP 中。也就是说，对于任何回答“否”的实例，存在一个多项式长度的证书使得可以在多项式时间内验证其正确性。

一个问题属于 co-NP，当且仅当它的补问题属于 NP。（不需要自身为NP）

Reduction相关概念¶

此题选A，iff

w∈L1 <=> f(w)∈L2

四个选项都需要背诵

NP-Hard and NP-Complete¶

所有的NP-Complete问题都是NP-Hard问题。

NP-Hard问题不一定是NP问题（可能甚至无法在多项式时间内验证），且所有的NP问题都可以在多项式时间内归约到NPH问题。
NPH并且NP可以推得NPC

Approximation¶

找到一个在多项式时间内得到近似解的算法

Approximation Ratio¶

不管是最小化问题还是最大化问题，ratio都是大于1的

fully polynomial-time approximation scheme (FPTAS)：
输入同时包括问题实例和误差参数ϵ，且最后的时间也是关于$1/ϵ$的多项式时间

Bin Packing（NPC）¶

Next Fit:O(N)¶

Next Fit只关注上一个桶

First Fit:O(Nlog(N))¶

First Fit会关注前面所有已有的桶

为了达到O(NlogN)的时间复杂度，可以使用堆或AVL树等结构存放每个桶的剩余容量

Best Fit¶

On-line Algorithm¶

仅根据当前情况来进行决策

Off-line Algorithms¶

概括来说就是先降序排序再使用First/Best Fit策略

The Knapsack Problem¶

fractional version¶

0-1 version（NPH）¶

背包中的物品不能切分，要么放要么不放

0-1背包的判定问题是npc，但是0-1背包是NPH

分别对0-1背包问题使用两种策略得到两个解，最后得到的结果取其中的最大值，则最后的approximation ratio = 2

$p_{max}$表示所有物品中价值最大的物品的价值
第二个不等式由maximum profit贪心策略得到
且$P_{frac}<=P_{greedy}+p_{max}$
事实上主要要猜测第三个不等式

0-1 version Dynamic Solution¶

这里提供了另一种动态规划的思路：从前i个物品中进行选择，使得在给定总价值的情况下的重量最小

pseudo-polynomial time：O(n*W)

这是因为n表示的是n个输入，但是W则是任意给定的数将输入视为“一组东西”，将大小视为“该阵列中有多少东西”。项输入实际上是数组中n个项的数组，因此size = n。容量输入不是其中的W数字数组，而是一个由log（W）位数组表示的单个整数。将它的大小增加1（加上1个有意义的位），W增加一倍，运行时间增加一倍，因此，指数时间复杂度增加。